Deep Learning on Nuclear Magnetic Resonance
ML4Sci
I left the last blog half an hour before a Machine Learning for Science event started. There were six events, and while I was tempted by the Google Earth competition, I really had to focus on the chemistry / solid state physics of the NMR event.
A Nickel of EDA
Basically, the goal was to go from simulated experimental data:
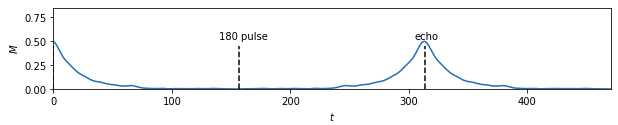

to four material properties (alpha, xi, p, and d):

Wading In
I took a broad approach. I really wanted to look at this data from a variety of angles, and that led me to automated machine learning (AutoML). As chronicled in my GitHub repo, I first attacked the problem with autosklearn, figuring that probably did not have the juice to really address the problem, but curious to find out what methods it would churn out as the best. It wound up being fairly hard to install, did not do as good as job as I’d hoped automating the preprocessing of data (it seemed to insist on treating continuous input values as categorical) and the results were really volatile, with adaboost, random forests, the “passive aggressive” regressor, and KNN methods all sometimes coming to the top. And the fits were bad. Still, it’s a tool I now know something about how to use for new problems.
Next I found AutoKeras, which is a little easier to install and a little better documented, for my purposes. It has the advantage of automating a search through some fairly high level options for setting up a Keras network. It, too, seems unable to believe I’d feed it straight numeric data and insisted on patching in some categorization tools. In any case, it got me started.
From there I moved on to kerastuner, which got me to reasonable models. Keras Tuner takes a structured description of a neural network and checks a manually designated set of options for things like layer width, activation function, learning rate, nearly all the hyperparameters of a neural network model. I ended up with my best scores (lowest weighted MSE losses) for a simple model with 900 input nodes to hold real and imaginary magnetization values at 450 time points and two hidden layers with 512 and 256 nodes to predict the 4 material properties. As you can see, the variables trained very differently:

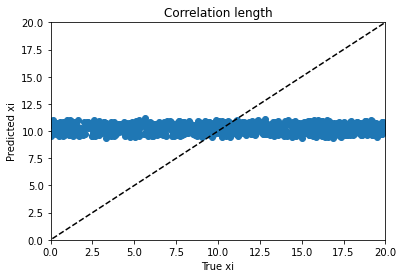
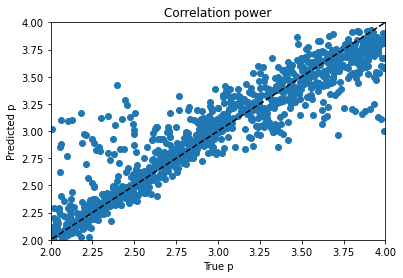
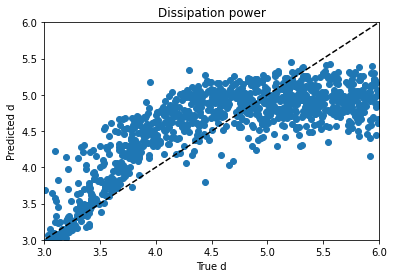
Alpha trains up very well; p trains ok, and varies with hyperparameter choice and training duration. Xi is can’t train won’t train; I would need to dig into the theory to find out more. d is maddening. Basically, it’s a decay factor, and it seems as if it’s predictable up to a value of about 4, and after that the length of the experiment is apparently wrong for the purpose of clarifying it. It looks like a bloody logarithmic curve in the real vs. predicted plots, and I tried applying transforms to change it, but I think that’s trying to apply a bandage to a problem that needs to be addressed earlier in the process somehow; again, digging into the theory of what’s going on would be essential.
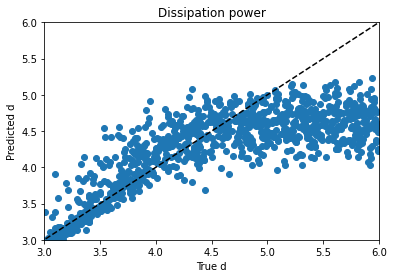
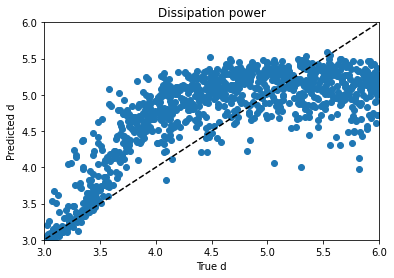
I tried regressing d by itself and using mean absolute error instead of a mean squared error metric, hoping for a plot where d lined up with predictions from 3 to 4 and then just flared out after that, which would be more sensible if I’m right about its behavior and its causes, but it didn’t look that different. Maddening. It’s one thing to jack around with the knobs and get unpredictable changes, but when no matter what you do to the knob you get the same problem, it’s frustrating.
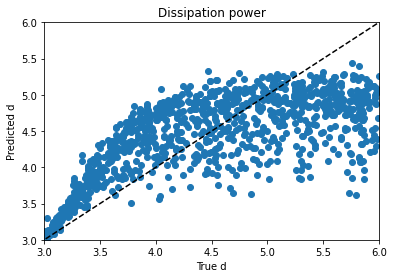
–PAG
Blogging platform assembled by Jekyll, Poole, and Zach Miller of Metis.